출처: 백준 알고리즘
주소: www.acmicpc.net/problem/11279
11279번: 최대 힙
첫째 줄에 연산의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 자연수라면 배열에 x라는 값을 넣는(추가하는) 연산이고, x가
www.acmicpc.net

문제 요약:
(1) 최대 힙 자료구조 생성
=> 힙의 최대 크기(N): 100000, 힙의 저장되는 자연수의 범위: 1 ~ 231 - 1
(2) x값이 0이면 힙에서 가장 큰 값 출력하고 그 값을 힙에서 제거
(3) x값이 자연수이면 힙에 삽입
문제 해결:
A. 자료구조 최대 힙을 정의
B. 최대 힙의 삽입 함수 생성
C. 최대 힙의 최대 값 삭제 함수 생성
자료구조 힙(heap) 설명:
1) 완전 이진 트리이며, 우선순위 큐를 위해 만들어진 자료구조이다.
=> 우선순위 큐: 데이터의 우선순위를 정해서 그 우선순위를 큐(Queue)에 적용
=> 우선순위를 max라고 정할 경우, 최대 값이 제일 먼저 나가게 된다.
=> 원래 큐는 제일 먼저 들어온 데이터가 제일 먼저 나간다.
2) 위 백준 문제처럼 max값이나 min값을 기준으로 일부만 정렬되었다.
=> 부모 노드가 자식 노드보다 우선순위(max, min)가 높은 자료구조이다.
3) 아래의 예시처럼 힙은 중복된 값을 가질 수 있다.

알고리즘:
A. 힙(heap) 자료구조 구현
- 크기가 100001인 배열 생성
=> 쉬운 구현을 위해 인덱스 1부터 시작
- 현재 노드의 인덱스가 i 이면
=> 왼쪽 자식 노드의 인덱스: 2 * i
=> 오른쪽 자식 노드의 인덱스: 2 * i + 1
=> 아래의 그림에서 현재 노드의 인덱스는 (i = 1)이다.

B. 최대 힙(heap)에 자연수 삽입 함수 생성
1. 새로운 자연수가 들어오면 힙(heap) 배열 사이즈 1 증가

2. 힙(heap) 배열의 맨 뒤에 새로운 자연수 삽입
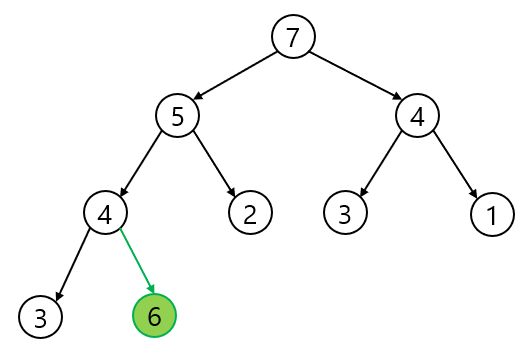
3. 새로운 자연수 > 새로운 자연수의 부모 노드의 값이면 새로운 자연수와 부모 노드와 교환
4. 새로운 자연수 <= 부모노드 일 때까지 3.번 반복

4-1. 4(부모 노드 값)와 6(새로운 자연수)을 교환
4-2. 5(부모 노드 값)와 6(새로운 자연수)을 교환
4-3. 7(부모 노드 값)와 6(새로운 자연수)는 교환하지 않음 (부모 노드 값이 더 크다)
C. 최대 힙(heap)에 제일 큰 값 삭제 함수 생성
1. 루트 값을 변수에 저장

2. 힙(heap) 배열의 맨 마지막 값을 루트 값에 저장

3. 힙(heap) 배열의 크기 1 감소

4. (마지막 값 < 마지막 값의 자식 노드 중 큰 값)이면 두 값 교환
5. (마지막 값 >= 마지막 값의 자식 노드 중 큰 값) 될 때까지 3.번 반복

6. 루트 값을 저장한 변수를 리턴
소스 코드:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
|
#include <iostream>
#define MAX_HEAP_LEN 100001
typedef struct {
long long int heap[MAX_HEAP_LEN];
int heap_size;
} Heap;
void insert_max_heap(Heap* h, long long int input_val) {
int i = ++(h->heap_size); // heap size 1 증가
// 맨 마지막에 값을 대입하고 트리를 거슬러 올라가면서 부모 노드와 비교
while ((i != 1) && (input_val > h->heap[i / 2])) {
// i번째 노드와 i번째의 부모 노드 교환
h->heap[i] = h->heap[i / 2];
// i의 부모 노드로 변경
i /= 2;
}
h->heap[i] = input_val;
}
long long int delete_max_heap(Heap* h) {
int child_idx, parent_idx;
long long int delete_val, last_val;
delete_val = h->heap[1]; // 삭제 값
last_val = h->heap[(h->heap_size)--]; // 마지막 값 저장, heap_size를 하나 줄임
parent_idx = 1; // 처음 부모 노드의 인덱스
child_idx = 2; // 처음 자식 노드의 인덱스
// 자식 노드의 인덱스가 heap_size보다 작은 경우 반복
while (child_idx <= h->heap_size) {
// 부모 노드의 자식 노드 중 더 큰 자식 노드 찾기
// 오른쪽 자식이 더 크면 child_idx 하나 증가
if ((child_idx < h->heap_size) && h->heap[child_idx] < h->heap[child_idx + 1]) {
child_idx++;
}
// 자식 노드보다 마지막 노드가 크거나 같으면
// while문 중지
if (last_val >= h->heap[child_idx]) {
break;
}
// 자식 노드보다 마지막 노드가 작으면
h->heap[parent_idx] = h->heap[child_idx];
parent_idx = child_idx;
child_idx *= 2;
}
// 마지막 노드 값 대입
h->heap[parent_idx] = last_val;
return delete_val;
}
int main() {
// 변수
long long int x, max_val;
Heap h;
int n;
// heap_size 초기화
h.heap_size = 0;
// 입력
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%lld", &x);
// 최대값 출력
if (x == 0) {
// heap_size가 0이면 0 출력
if (h.heap_size == 0) {
max_val = 0;
}
// heap_size가 0보다 크면
else {
max_val = delete_max_heap(&h);
}
printf("%lld\n", max_val);
}
// x값 입력
else {
insert_max_heap(&h, x);
}
}
return 0;
}
|
cs |
한줄평:
-> 자료구조에 대해 이해하고 직접 구현하면 나중에 코딩문제에 적용할 수 있을 것 같다.
'알고리즘 > 백준' 카테고리의 다른 글
| 11286번 - 절댓값 힙 (0) | 2021.04.06 |
|---|---|
| 1927번 - 최소 힙 (0) | 2021.04.05 |
| 1300번 - K번째 수 (0) | 2021.03.30 |
| 2110번 - 공유기 설치 (0) | 2021.03.29 |
| 11401번 - 이항 계수 3 (0) | 2021.03.01 |



