출처: 백준 알고리즘
주소: www.acmicpc.net/problem/1260
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net

문제 요약:
(1) 입력으로 정점의 개수(N), 간선의 개수(M), 탐색을 시작할 정점의 번호(V)를 제공
=> (각 입력의 범위는 N: 1 ~ 1000, M: 1 ~ 10000, V: 1 ~ N 이다.)
(2) 이후 M개의 간선을 입력으로 제공한다.
(3) 입력으로 제공된 정보를 이용하여 DFS을 수행한 결과 출력
(4) 또한, BFS를 수행한 결과 출력
=> (3)과 (4)을 수행할 때, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 순으로 방문
문제 해결:
A. 정점이라는 것을 Vertex 구조체로 정의
B. DFS와 BFS의 클래스 정의
C. 각 클래스에 입력 함수 및 수행 함수 정의
미리 공부할 내용:
(1) Depth First Search(DFS): 깊이 우선 탐색
- 그래프나 트리를 탐색을 할 때, 사전에 정의된 깊이를 우선적으로 탐색을 하는 알고리즘을 말한다.
- 간단하고 이해하기 쉬운 트리를 통해 이해해보자.
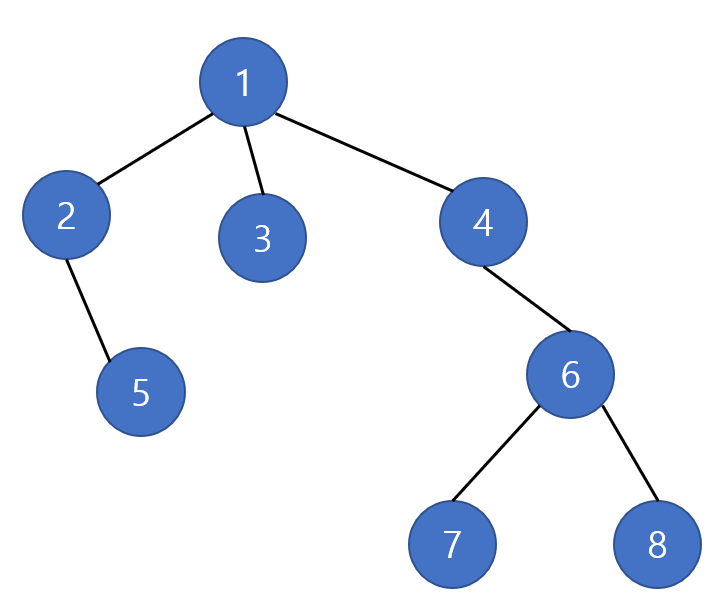
- 1에서 시작해서 8을 찾는 예시
=> (가정: 자식 노드로 내려온 경우는 작은 수 먼저 탐색을 한다)
=> 먼저, 1에서 시작한다.

=> 1을 탐색 후, 8이 아니여서 1에 방문표시를 해놓고, 갈 곳을 정해 놓는다.
=> 그 중에서 제일 작은 값부터 방문한다.
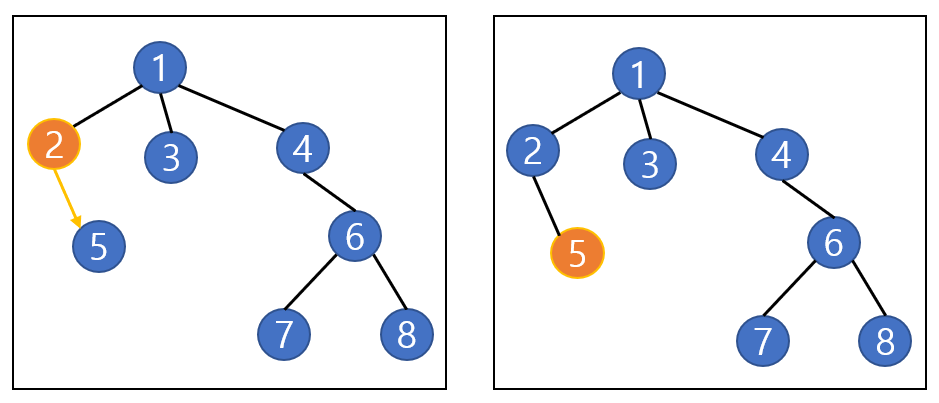
=> 2와 5를 같은 방식으로 방문한다.
=> 그 후 3과 4 등을 방문한다.

=> 차례로 방문을 하고 마지막에 8을 찾게 된다.
- DFS의 장점
=> 만약 찾고자 하는 값이 깊은 곳에 존재하는 경우 해를 빨리 구할 수 있다.
- DFS의 단점
=> 해가 없는 경로의 끝까지 가는 경우가 발생한다.
=> 해를 탐색한 순서가 최단 경로라는 보장이 없다.
(위 예시를 보더라도 1 -> 4 -> 6 -> 8이 제일 빠른 방법인데, 다른 곳도 끝까지 탐색을 하다보니 오래 걸리게 된다.)
(2) Breadth First Search(BFS): 너비 우선 탐색
- 그래프나 트리를 탐색을 할 때, 사전에 정의된 너비를 우선적으로 탐색을 하는 알고리즘을 말한다.
- 간단하고 이해하기 쉬운 트리를 통해 이해해보자.
- 1에서 시작해서 8을 찾는 예시
=> (가정: 자식 노드로 내려온 경우는 작은 수 먼저 탐색을 한다)
=> 먼저, 1에서 시작한다.

=> 1을 탐색 후, 8이 아니여서 1에 방문표시를 해놓고, 갈 곳을 정해 놓는다.
=> 그 중에서 작은 값부터 모든 자식 노드를 방문한다.

=> 모든 자식 노드를 방문하면서 자식 노드의 자식 노드의 값을 저장해놓는다.
=> 이후, 저장해 놓은 값에서 작은 값부터 모두 방문한다.

=> 5와 6을 방문하면서 자식 노드의 값을 저장해놓는다.
=> 이후, 저장해 놓은 값에서 작은 값부터 모두 방문한다.

=> 7와 8을 방문해서 찾고자하는 값인 8을 찾았다.
- BFS의 장점
=> 찾은 경로가 시작 노드에서 끝 노드까지의 최단 경로를 보장한다.
(1 -> 4 -> 6 -> 8 이로 인해, 최단 경로을 얻을 수 있게 되었다.)
- BFS의 단점
=> 찾고자 하는 값이 깊은 곳에 위치하게 되면 모든 너비를 탐색하기 때문에 오래 걸리게 된다.
=> 또한, 가고자 하는 값을 저장해야하므로 기억공간이 DFS보다 많이 필요하게 된다.
알고리즘:
A. 정점이라는 것을 Vertex 구조체로 정의
=> 정점을 나타내는 구조체를 선언한다.
=> 구조체에는 해당 정점을 방문(visit)여부를 판단하는 변수를 저장
=> 해당 정점의 이웃(neighbor)을 vector를 통해 저장하였다.
|
typedef struct Vertex {
bool visit;
std::vector<int> neighbor;
};
|
cs |
B. DFS와 BFS의 클래스 정의
- DFS 클래스
- 변수
=> Vertex 타입 배열 v를 설정
- 함수
=> 값을 배열 v에 입력하는 함수(InputNei)
-> 반환값 없음, 입력 값(int insert_idx, int insert_val)
-> 배열 v에 입력할 값(insert_val)를 해당 위치(insert_idx)에 대입
=> 값을 찾는 함수(Search)
-> 반환값 없음, 입력값(int start_idx)
-> 시작 위치(start_idx)에서 탐색을 하여 끝날 때까지의 값을 출력
|
// DFS (Depth First Search)
class DFS {
private:
Vertex v[MAX_N_LEN+1];
public:
void InputNei(int insert_idx, int insert_val);
void Search(int start_idx);
};
|
cs |
- BFS 클래스
- 변수
=> Vertex 타입 배열 v를 설정
- 함수
=> 값을 배열 v에 입력하는 함수(InputNei)
-> 반환값 없음, 입력 값(int insert_idx, int insert_val)
-> 배열 v에 입력할 값(insert_val)를 해당 위치(insert_idx)에 대입
=> 값을 찾는 함수(Search)
-> 반환값 없음, 입력값(int start_idx)
-> 시작 위치(start_idx)에서 탐색을 하여 끝날 때까지의 값을 출력
|
// BFS (Breadth First Search)
class BFS {
private:
Vertex v[MAX_N_LEN+1];
public:
void InputNei(int insert_idx, int insert_val);
void Search(int start_idx);
};
|
cs |
C. 각 클래스에 입력 함수 및 수행 함수 정의
- DFS나 BFS나 값을 삽입하는 함수의 방식은 같다.
=> 삽입할 위치에 삽입하고자 하는 값을 넣는 방식이다.
- DFS 함수
(1) 시작 위치에 방문 표시
(2) 시작 위치 출력
(3) 시작 위치의 이웃 정점들을 정렬
=> 정렬하는 이유는 "방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 순으로 방문" 하기 때문이다.
(4) 값이 작은 이웃 정점들부터 방문 여부 판단
(4-1) 방문하지 않은 경우, 해당 위치부터 DFS 함수 재귀 호출
- 함수 코드:
|
// 시작 위치(start_idx)부터 DFS 하는 함수
void DFS::Search(int start_idx) {
// (1) 시작 위치에 방문 표시
v[start_idx].visit = true;
// (2) 시작 위치 출력
printf("%d ", start_idx);
// (3) 이웃의 정점을 정렬
std::sort(v[start_idx].neighbor.begin(), v[start_idx].neighbor.end());
// (4) 값이 작은 이웃부터 반복
for (int i = 0; i < v[start_idx].neighbor.size(); i++) {
// (4) 다음 위치 계산
int next = v[start_idx].neighbor[i];
// (4-1) 다음 위치를 방문하지 않았으면
if (!v[next].visit) {
// (4-1) DFS 함수 재귀
DFS::Search(next);
}
}
}
|
cs |
- DFS 함수
(1) 탐색할 위치들을 저장하는 queue 변수 설정
(2) 시작 위치 queue 변수에 삽입
(3) 시작 위치 방문 표시
(4) 탐색할 위치들을 저장하는 queue가 비어있지 않는 동안 반복
(4-1) queue의 처음 값을 저장하고 출력 후, queue에서 제거
(4-2) queue의 처음 값의 이웃들을 정렬
=> 정렬하는 이유는 "방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 순으로 방문" 하기 때문이다.
(4-3) 값이 작은 이웃부터 반복
(4-3-1) 다음에 방문할 위치 찾기
(4-3-2) 방문할 위치를 방문하지 않은 경우 해당위치를 방문 표시를 한 후, queue에 삽입
- 함수 코드:
|
// 시작 위치(start_idx)부터 BFS 하는 함수
void BFS::Search(int start_idx) {
// (1) 탐색할 위치들을 저장하는 queue 변수 설정
std::queue<int> q;
// (2) 시작 위치 queue 변수에 삽입
q.push(start_idx);
// (3) 시작 위치 방문 표시
v[start_idx].visit = true;
// (4) 탐색할 위치들을 저장하는 queue가 비어있지 않는 동안 반복
while (!q.empty()) {
// (4-1) queue의 처음 값을 저장
int cur = q.front();
// (4-1) queue에서 제거
q.pop();
// (4-1) queue의 처음 값 출력
printf("%d ", cur);
// (4-2) queue의 처음 값의 이웃들을 정렬
std::sort(v[cur].neighbor.begin(), v[cur].neighbor.end());
// (4-3) 값이 작은 이웃부터 반복
for (int i = 0; i < v[cur].neighbor.size(); i++) {
// (4-3-1) 다음에 방문할 위치 찾기
int next = v[cur].neighbor[i];
// (4-3-2) 다음에 방문할 위치를 방문하지 않았을 경우
if (!v[next].visit) {
// (4-3-2) 해당 위치를 방문 표시
v[next].visit = true;
// (4-3-2) 해당 위치를 queue에 삽입
q.push(next);
}
}
}
}
|
cs |
소스 코드(전체적인 코드):
|
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#define MAX_N_LEN 1000
typedef struct Vertex {
bool visit;
std::vector<int> neighbor;
};
// DFS (Depth First Search)
class DFS {
private:
Vertex v[MAX_N_LEN+1];
public:
void InputNei(int insert_idx, int insert_val);
void Search(int start_idx);
};
// 입력 값(insert_val)을 해당 위치(insert_idx)에 넣는 함수
void DFS::InputNei(int insert_idx, int insert_val) {
v[insert_idx].visit = false;
v[insert_idx].neighbor.push_back(insert_val);
}
// 시작 위치(start_idx)부터 DFS 하는 함수
void DFS::Search(int start_idx) {
// (1) 시작 위치에 방문 표시
v[start_idx].visit = true;
// (2) 시작 위치 출력
printf("%d ", start_idx);
// (3) 이웃의 정점을 정렬
std::sort(v[start_idx].neighbor.begin(), v[start_idx].neighbor.end());
// (4) 값이 작은 이웃부터 반복
for (int i = 0; i < v[start_idx].neighbor.size(); i++) {
// (4) 다음 위치 계산
int next = v[start_idx].neighbor[i];
// (4-1) 다음 위치를 방문하지 않았으면
if (!v[next].visit) {
// (4-1) DFS 함수 재귀
DFS::Search(next);
}
}
}
///////////////////////////////////////////
// BFS (Breadth First Search)
class BFS {
private:
Vertex v[MAX_N_LEN+1];
public:
void InputNei(int insert_idx, int insert_val);
void Search(int start_idx);
};
// 입력 값(insert_val)을 해당 위치(insert_idx)에 넣는 함수
void BFS::InputNei(int insert_idx, int insert_val) {
v[insert_idx].visit = false;
v[insert_idx].neighbor.push_back(insert_val);
}
// 시작 위치(start_idx)부터 BFS 하는 함수
void BFS::Search(int start_idx) {
// (1) 탐색할 위치들을 저장하는 queue 변수 설정
std::queue<int> q;
// (2) 시작 위치 queue 변수에 삽입
q.push(start_idx);
// (3) 시작 위치 방문 표시
v[start_idx].visit = true;
// (4) 탐색할 위치들을 저장하는 queue가 비어있지 않는 동안 반복
while (!q.empty()) {
// (4-1) queue의 처음 값을 저장
int cur = q.front();
// (4-1) queue에서 제거
q.pop();
// (4-1) queue의 처음 값 출력
printf("%d ", cur);
// (4-2) queue의 처음 값의 이웃들을 정렬
std::sort(v[cur].neighbor.begin(), v[cur].neighbor.end());
// (4-3) 값이 작은 이웃부터 반복
for (int i = 0; i < v[cur].neighbor.size(); i++) {
// (4-3-1) 다음에 방문할 위치 찾기
int next = v[cur].neighbor[i];
// (4-3-2) 다음에 방문할 위치를 방문하지 않았을 경우
if (!v[next].visit) {
// (4-3-2) 해당 위치를 방문 표시
v[next].visit = true;
// (4-3-2) 해당 위치를 queue에 삽입
q.push(next);
}
}
}
}
int main() {
// 변수 선언
// n: 정점의 개수
// m: 간선의 개수
// v: 탐색을 시작할 정점 번호
// lv: 입력받은 왼쪽 정점
// rv: 입력받은 오른쪽 정점
int n, m, v, lv, rv;
DFS dfs;
BFS bfs;
scanf("%d %d %d", &n, &m, &v);
for (int i = 0; i < m; i++) {
scanf("%d %d", &lv, &rv);
dfs.InputNei(lv, rv);
dfs.InputNei(rv, lv);
bfs.InputNei(lv, rv);
bfs.InputNei(rv, lv);
}
dfs.Search(v);
printf("\n");
bfs.Search(v);
printf("\n");
return 0;
}
|
cs |
한줄평:
-> 탐색의 두가지를 이해하고 코드로 작성해봄으로써 더욱 잘 이해할 수 있다.
'알고리즘 > 백준' 카테고리의 다른 글
| 1753번 - 최단경로 (0) | 2021.07.01 |
|---|---|
| 2667번 - 단지번호붙이기 (0) | 2021.04.13 |
| 1655번 - 가운데를 말해요 (0) | 2021.04.08 |
| 11286번 - 절댓값 힙 (0) | 2021.04.06 |
| 1927번 - 최소 힙 (0) | 2021.04.05 |



